
En este post vamos a comentar seis metodologías posibles para la atribución multicanal.
En todos los casos que vamos a ver, la situación es la misma: queremos poder explicar, de entre un montón de puntos de contacto que existieron entre los consumidores y nuestra publicidad, gracias a cuáles de ellos se produjo una acción que nos interesa (visitar nuestra página web, pedir un presupuesto, comprar, etc.).
Para simplificar el discurso, nos centramos en una variable objetivo única: comprar.
Veamos los diferentes enfoques.
- Regresión logística
La variable objetivo es binaria (si/no) y se modeliza en función del número de veces que las personas han pasado por delante de la publicidad.
Gracias a la tecnología, sabemos el número de veces que una persona (en realidad el dispositivo que la persona está utilizando para navegar por Internet) ha pasado por las páginas en las que tenemos nuestros anuncios (X1, X2,…Xn).
Además, sabemos si entró en nuestra página web y cómo fue su navegación (Z1, Z2,…Zk).
Finalmente, sabemos si compró o no (Y=1 o 0).
Modelizamos Y en función de X y Z.
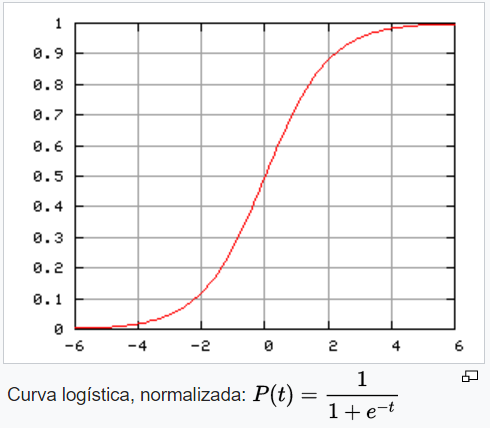
Una de las ventajas que tiene este enfoque es que es muy sencillo de entender.
Y quizás el principal punto débil es que no tiene en cuenta el tiempo. Es decir, si tu has pasado 3 veces por delante de un anuncio de display en El País ayer, y también has pasado 3 veces por delante del mismo anuncio de display en El Mundo hace una semana, el método de regresión logística dará la misma importancia a uno que a otro.
- Regresión logística con remuestreo
En nuestro segundo método de atribución, en lugar de una sola regresión logística sobre una muestra N, se divide la muestra en K submuestras (N1, N2,… Nk), se hacen regresiones logísticas para cada submuestra y se toman como coeficientes los promedios de las K regresiones.
- Modelo de análisis de supervivencia
Mejora los dos enfoques anteriores porque sí tiene en cuenta el tiempo en que tienen lugar las interacciones.
Igual que en el caso de arriba, tenemos todos los recorridos de personas que han pasado por delante de la publicidad. Necesitamos discernir la atribución que se da de las compras a todos y cada uno de ellos.
Vamos a suponer que cogemos todos los recorridos en los últimos 350 días. Supongamos que esos recorridos fueran 1000. Dividimos los 1000 recorridos en 400 que pasaron por delante de nuestros anuncio display en El País y 600 que no pasaron por delante de dicho anuncio.
El análisis consiste en ver, por ejemplo, cada determinado número de días, cuántos de esos recorridos no llegaron a nuestra función objetivo (comprar) en uno y otro subconjunto y compararlos.
Por ejemplo, en los primeros 100 días, del grupo 1 (sí pasaron por delante del anuncio del País) se cayeron (no compraron) 15. Del grupo 2 (no pasaron por El País), se cayeron 18. Así continuamente.
Finalmente obtenemos una gráfica como la que os muestro a continuación, donde vemos como el grupo 1 tiene más probabilidad de sobrevivir, en este caso comprar y, por tanto poner display en El País sería más efectivo que no ponerlo.
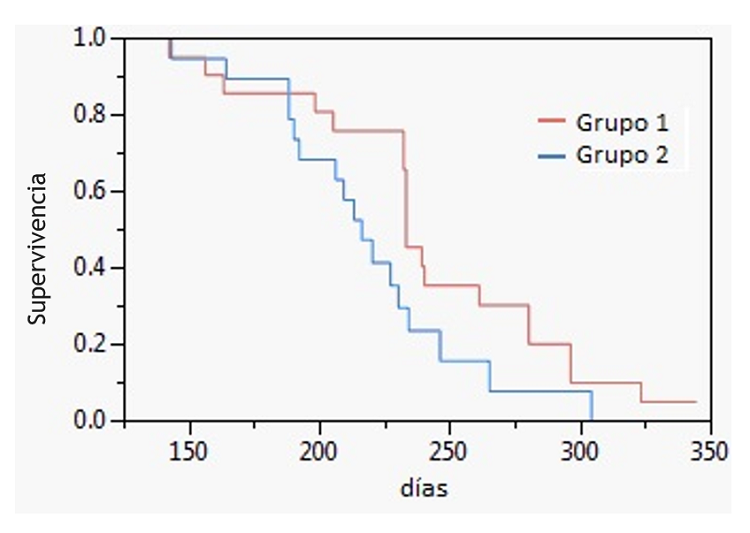
Para los que quieran profundizar un poco más en el tema, hay dos posibles modelos: Modelo de azar proporcional de Cox y Modelo de supervivencia de Kaplan-Meier.
- Análisis de grupos
Este enfoque se basa en la crítica a la estadística tradicional cuando el problema que se tiene entre manos es de decenas de millones de registros.
Consideran que en estos casos es mejor trabajar solo con aquellos grupos de personas que representan comportamientos similares de miles de personas.
Así, una vez determinados los grupos homogéneos entre sí y heterogéneos entre ellos, los centroides de los mismos permiten definir usuarios que actúan como representantes de miles de usuarios.
De esta forma, por ejemplo, no mezclaríamos en el mismo saco una persona con una gran actividad en Internet, que otra que casi no tenga actividad. O personas que han hecho clic en una búsqueda con aquellas que han hecho clic en display.
El algoritmo de identificación de grupos más popular es el K-medias:
- Se define el número de grupos que se quiere encontrar y se sitúan de manera aleatoria los centroides (representantes) de cada grupo. Las observaciones se asocian al centroide más cercano
- Se recalculan las posiciones de cada centroide con arreglo a las observaciones que le están asignadas y se reasignan las observaciones al centroide más cercano
- Se itera hasta que la posición de los centroides se estabiliza
- Se recomienda repetir el proceso con diferentes posiciones de partida y comparar los resultados

- Cadenas ocultas de Markov
Una cadena de Markov tiene la propiedad de que la probabilidad de que suceda algo (compra en nuestro caso) en el instante t sólo depende del estado en que se encontraba el sistema en el instante t-1, y no de los anteriores a este último.
Por ejemplo, si una persona hace compra un producto dado en la página web, qué hizo esa persona justo antes. Mejor aún, si 1000 personas han comprado un producto en la página web en el día de hoy, qué contactos hubo ayer entre nuestra publicidad y cada una de las 1000 personas, sin importar lo que pasó antes de ayer.
En el caso de la atribución multicanal, las cadenas de Markov se aplican a cada una de las etapas del embudo de conversión.
Las cadenas ocultas de Markov se caracterizan porque los estados (en nuestro caso por dónde navegó la persona) no son visibles directamente, sino que sólo lo son las variables influidas por el estado (por ejemplo, sabemos que alguien compró).
- Teoría de juegos y valor de Shapley
El valor de Shapley define la forma de repartir las ganancias entre los distintos jugadores aliados en un juego colaborativo. La recompensa para cada jugador debe estar relacionada con su contribución a la coalición.
Me gusta poner el ejemplo de un equipo de escaladores que juegan a conseguir un tesoro escondido en la cima. El juego es colaborativo, es decir, todos quieren conseguirlo en conjunto, no importando quién sea el que realmente llegue a él. El premio se da después en función de la participación de cada uno al éxito final.
Se basa en cuatro condiciones:
- Todas las ganancias son repartidas entre los jugadores
- Si la contribución de dos jugadores es idéntica, su recompensa es la misma
- Si un jugador no contribuye, su recompensa es cero
- Los jugadores que más contribuyen a la coalición, reciben más recompensa
En el caso de la atribución:
- Los jugadores son cada uno de los puntos de contacto
- Las ganancias son las conversiones (compra en nuestro caso)
- La recompensa es la atribución a cada punto de contacto
Todos estos métodos se utilizan de manera fácil e inmediata con datos de navegación online. Los datos offline se suelen meter con probabilidades. Es decir, entre dos puntos de contacto online pudo haber un anuncio en la TV y, por tanto, la probabilidad de ser impactado.




Comentarios