
Me gusta decir que la matemática es un idioma diferente, que dice lo mismo que otro idioma, pero que suena distinto. Creo que con el ejemplo que os voy a contar ahora os podéis hacer una idea de a qué me refiero.
Imaginaros hace 20 o 30 años, que vuestro padre hubiera querido llevar a vuestra madre a cenar a un restaurante nuevo el día de su aniversario. Posiblemente no hubiera querido arriesgarse a elegir mal, así que hubiera preguntado a todos los amigos, a ver quién conocía el restaurante y qué opinión tenía. De todas las opiniones se hubiera hecho una situación de lugar y hubiese decidido si ir o no. Pues esto mismo es lo que hacen los algoritmos de clasificación. Analizan todos los comentarios que las personas han hecho sobre un restaurante y obtienen una valoración promedio del restaurante, que ponen a disposición de la gente.
Existen gran variedad de estilos de clasificación. Desde la más sencilla, que suele ser determinar si una opinión es positiva o negativa. Hasta muchas otras como pueden ser: la decisión de si un e-mail debe o no ir a la bandeja de spam; clasificar una página web en función del tipo de contenidos que tiene; determinar de qué raza es un perro del que tenemos una foto; o dar un diagnóstico médico a un paciente (esto, por ejemplo, se ha hecho toda la vida en función de la temperatura, los análisis clínicos o los Rayos-X, pero ahora añadimos cosas como el ADN o el tipo de actividad que las personas realizamos cada día).
El Modelo de Clasificación más sencillo de todos es el lineal simple. Se utiliza para el análisis de textos y consiste en establecer a priori una serie de palabras positivas y negativas para luego contarlas sobre cada texto que se vaya a analizar, dando resultado positivo si son más las palabras positivas que las negativas, y viceversa. Lógicamente, su simplicidad hace que tenga muchos problemas: ¿cómo determinar qué palabras, cuántas? ¿Cómo distinguir si una palabra es más que otra, por ejemplo, «excelente» más que «bueno»? Si una opinión es «no bueno», ¿contará la palabra «bueno» como positiva?
Una mejora sencilla consiste en asignar pesos a cada palabra, en función de la importancia que queramos darle. Vemos un ejemplo en la Fig.1:
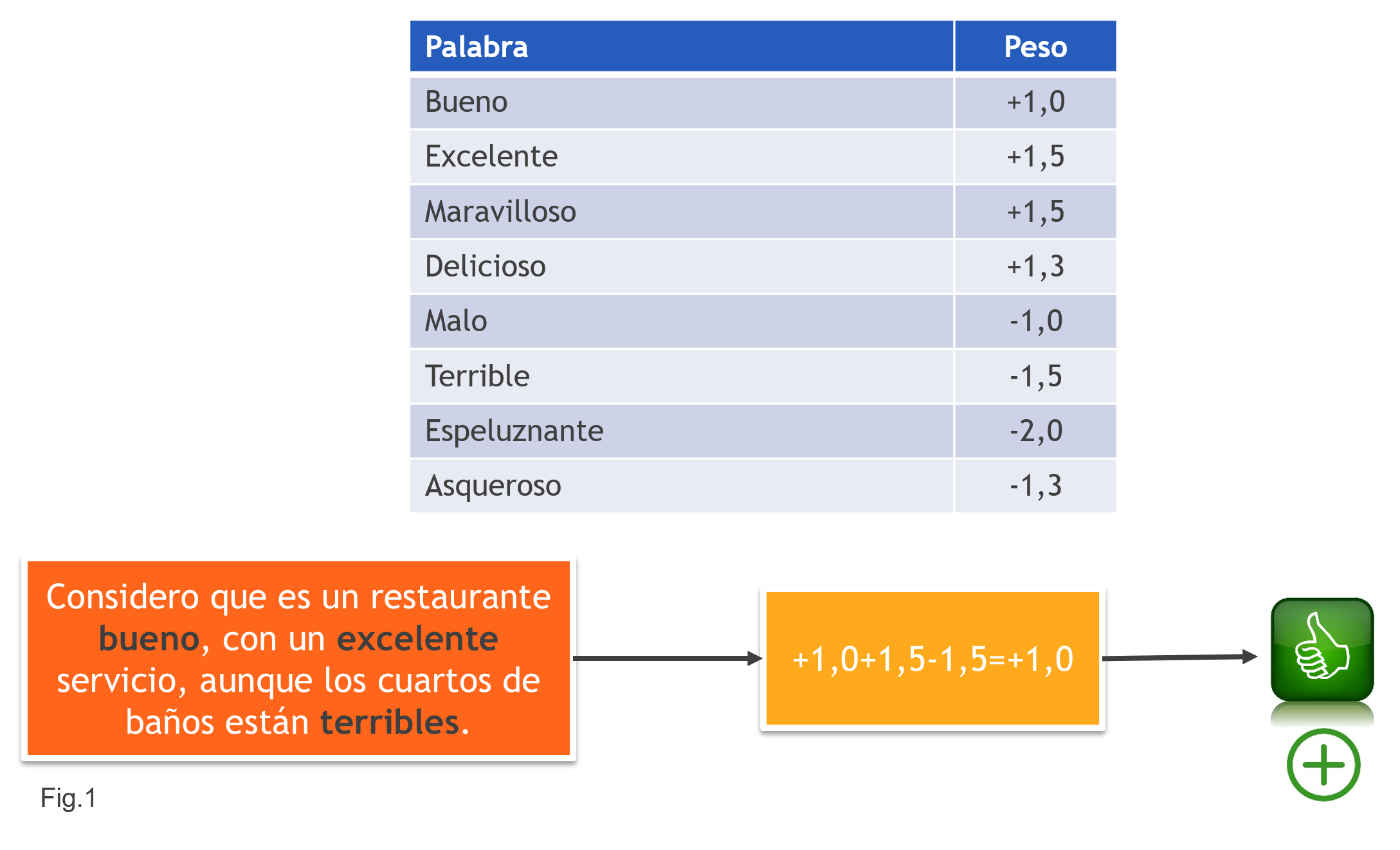
En este caso, la credibilidad del sentimiento es mayor.
Una manera gráfica de ver qué está pasando, cómo son las cosas, es dibujar en dos ejes dos palabras (por ejemplo «Bueno» y «Terrible») y situar puntos tales que cada uno de ellos refleje la cantidad de veces que en un comentario se ha dicho la palabra «Bueno» (Eje X) o la palabra «Terrible» (Eje Y). Si la importancia que damos a cada una de estas palabras es la de la tabla de la Fig.1, la línea 1,0″Bueno»-1,5″Terrible» es tal que todo lo que está debajo de ella son comentarios positivos y lo que está por encima, negativos. Esto es lo que se conoce como la Frontera de Decisión. Cuando graficamos solo dos variables es una línea recta; si fueran tres sería una plano y más de tres un hiperplano. Vemos un ejemplo en la Fig.2.
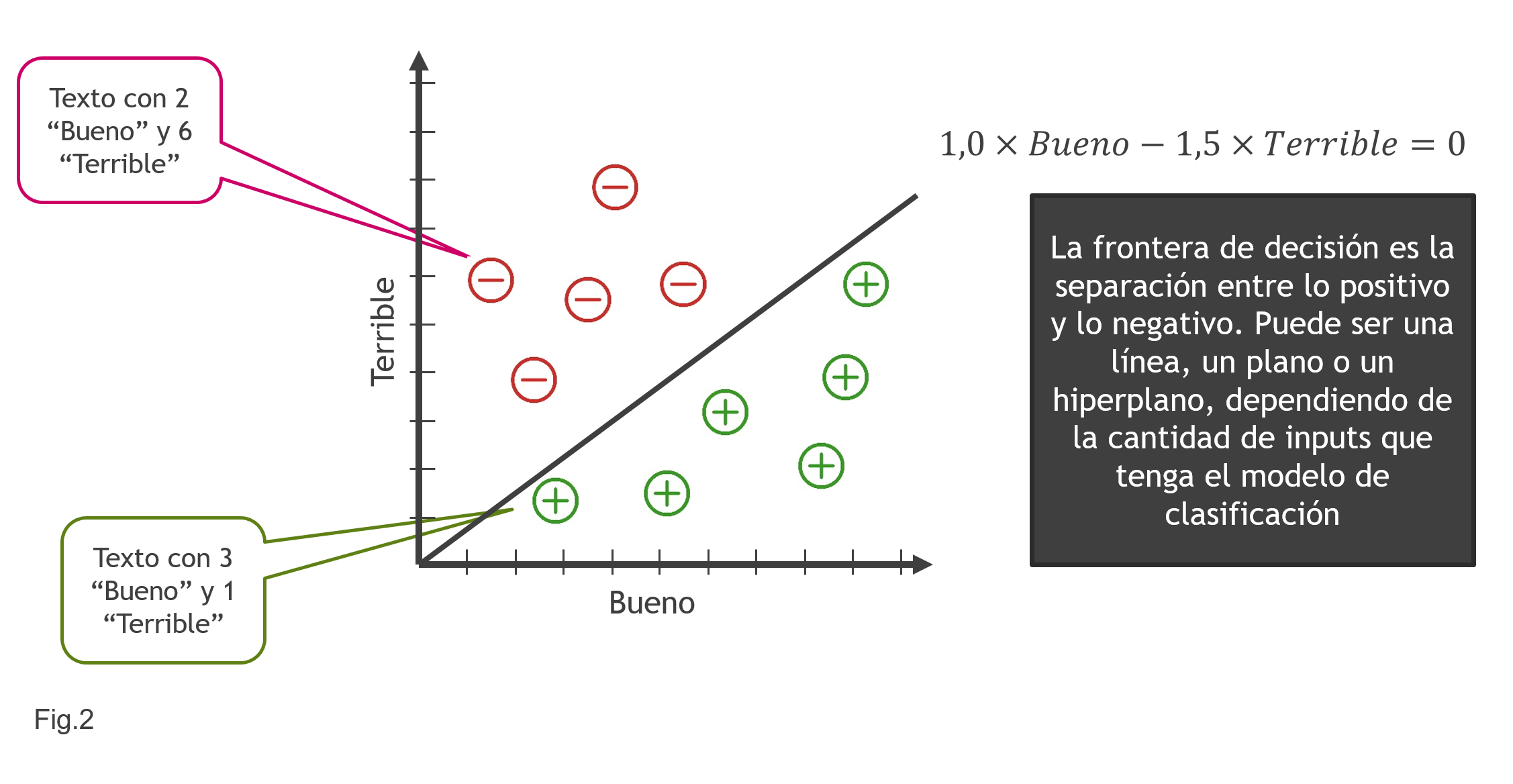
Ahora bien, llegados a este punto, ¿cómo saber si un modelo de clasificación es «de fiar»? Ya sabemos que en estadística cada cosa que uno hace tiene que llevar asignada una valoración del error o «riesgo» que se corre. En este tipo de modelos, como en muchos otros, se trabaja con un grupo de entrenamiento y un grupo de test. Con el primero se construye el modelo y se prueba en el segundo para ver si funciona bien. Por ejemplo, imaginemos que seguimos en el ejemplo de arriba y que el resultado 1,0″Bueno»-1,5″Terrible» lo hemos inferido de un grupo de entrenamiento. Imaginemos ahora que tenemos la siguiente opinión en el grupo de test «El servicio era bueno y la comida terriblemente deliciosa». Si aplicamos el Modelo de Clasificación saldrá que es un comentario negativo, pues tiene una vez la palabra «Bueno» y una vez la palabra «Terrible», es decir, una puntuación de -0,5. Sin embargo, es un comentario positivo, así que en este caso el modelo está cometiendo un error. La métrica global que se utiliza es la suma de todos los errores en el grupo test dividido sobre el total de opiniones en el grupo test.
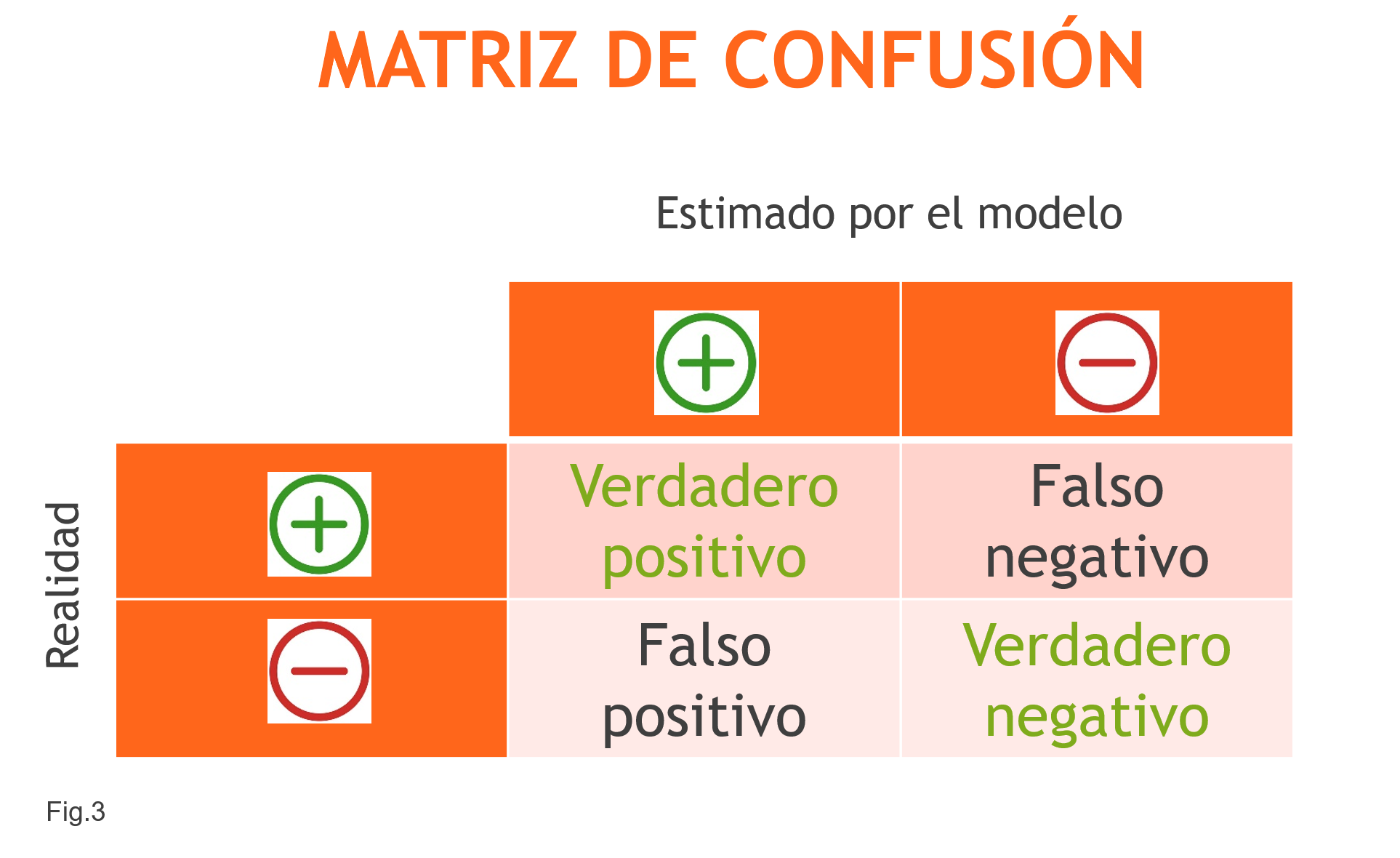
El ejemplo que acabamos de ver es lo que se denomina Falso Negativo (sale negativo pero es falso). Existe el caso contrario, Falso Positivo (sale positivo pero es falso). Ver todos los casos buenos y también estos dos tipos de errores es algo interesante y que aporta información. Se puede visualizar en un matriz como la de la Fig.3, que se denomina Matriz de Confusión.
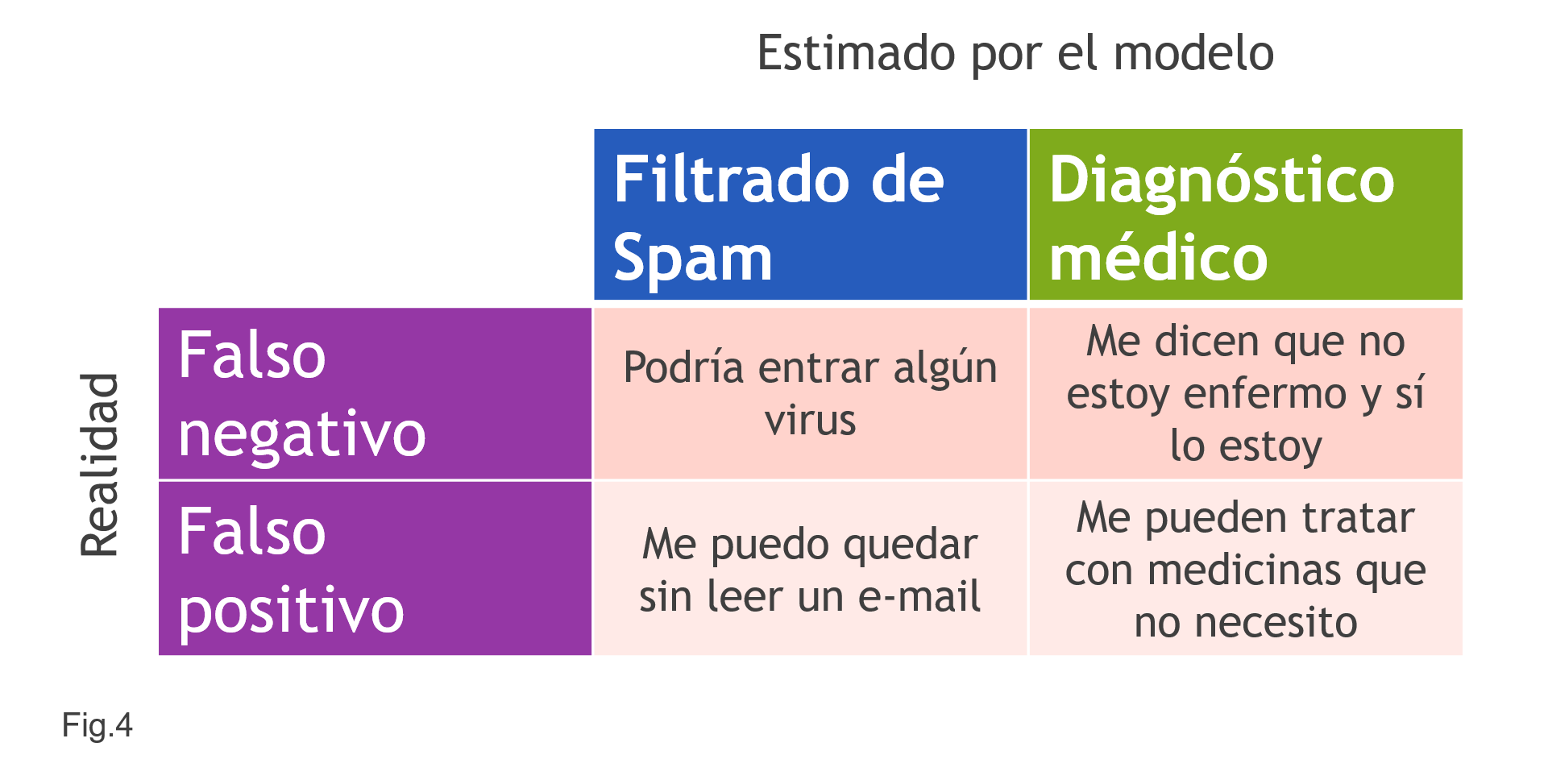
A pesar de tener estas métricas sencillas, sigue siendo difícil decir qué nos hace sentirnos conformes con un dato de error. Cada situación es diferente. Mirad por ejemplo el caso de la Fig.4. No es lo mismo cuando se trata de cosas generales que cuando se trata de cosas que afectan a uno personalmente.
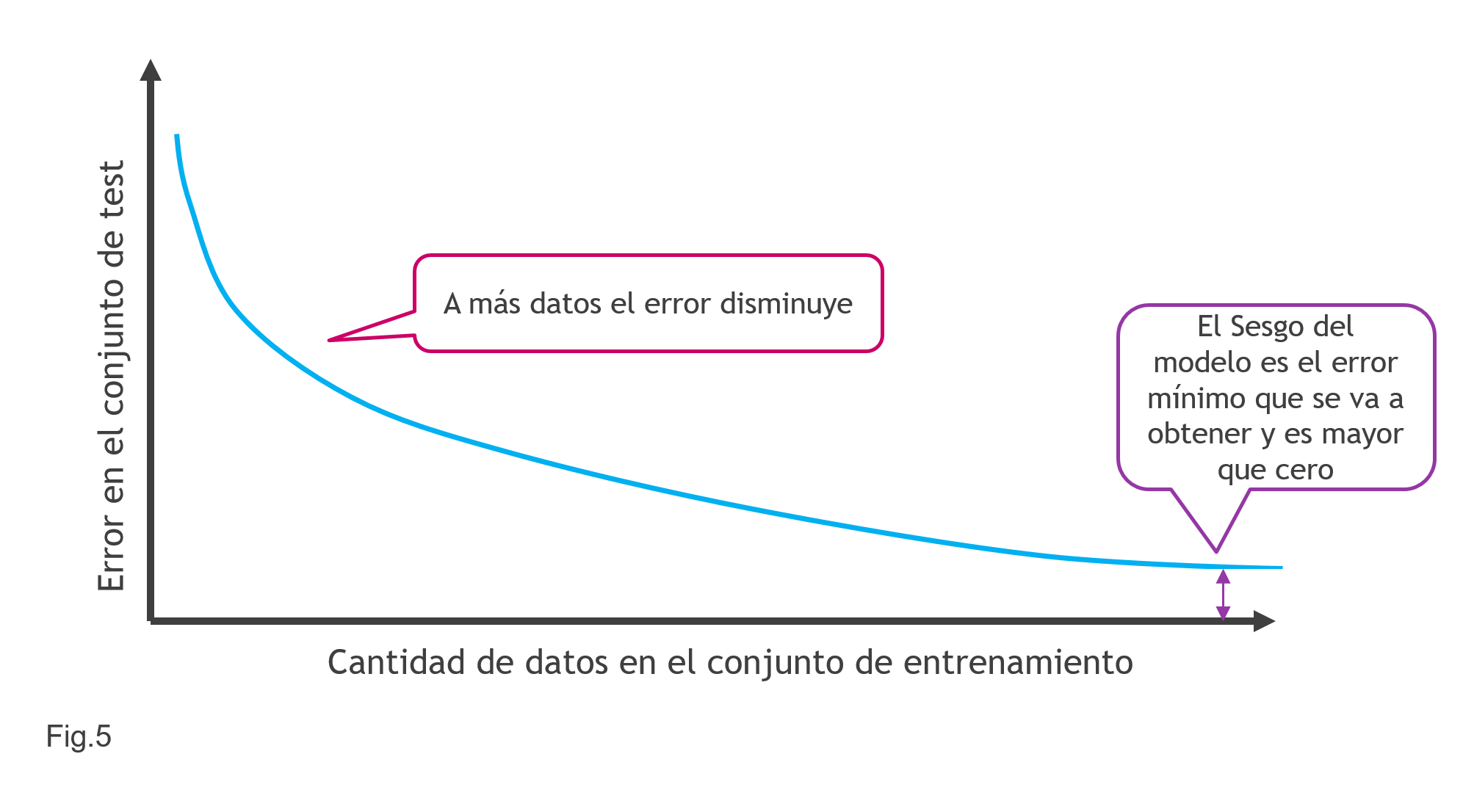
Está claro que a más datos el error será menor pero solo si los datos son buenos. A veces «por engordar la vaca la acabamos matando». La relación que existe en el Modelo de Clasificación Lineal entre la cantidad de datos es como se muestra en la Fig.5, que confirma que, a más datos menor error, pero que pone además de manifiesto que por muchos que sean los datos siempre va a existir lo que se denomina el Sesgo del modelo, que es el error mínimo que siempre se va a obtener.
Estos modelos de clasificación se están utilizando cada vez más para analizar Big Data y poder pasar de texto o imágenes a números que nos permitan clasificar, valorar y tomar decisiones.



Comentarios