
Imaginaros que tenéis que cuantificar cómo de similares son los siguientes dos textos:
- Me gustan las manzanas y las peras. Las manzanas, menos que las peras.
- Me gustan las flores y las especias. Las especias, menos que las flores.
Lo más simple sería contar cuántas veces aparece cada palabra en cada texto y buscar una forma de representar las comunes de alguna manera. Vamos a empezar poquito a poco.
Primero, representemos con un vector cada texto, poniendo en la primera columna cada palabra y en la segunda, las veces que aparece dicha palabra en el texto. Lo vemos en la Fig1.
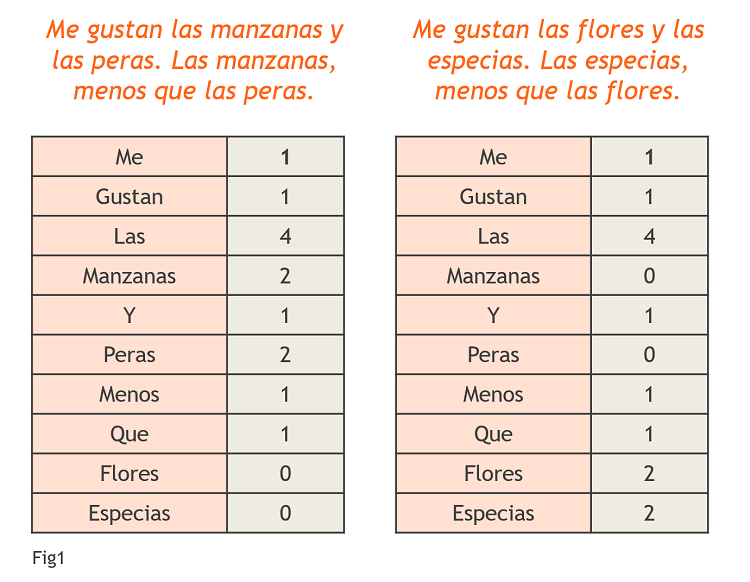
Una forma de representar lo cerca que están uno de otro es construir un nuevo vector con coordenadas cada palabra y el valor de las coordenadas la multiplicación de los vectores anteriores. De esta forma, si una palabra se repite mucho en el texto (imaginemos que se repite 10 veces) y nada en el otro (0), contará 10*0=0 veces en el nuevo vector que nos va a dar el grado de parecido. Si sumamos todas las coordenadas de este nuevo vector, tenemos una primera medida de la similitud entre las dos frases. Lo vemos en la Fig2.
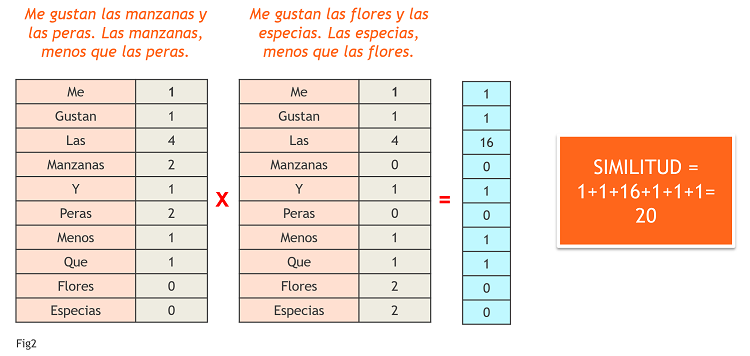
Este método se conoce como el método de conteo y, aunque sencillo, tiene un problema evidente: la independencia del tamaño del texto. Es decir, imaginemos que duplicamos los dos textos anteriores y volvemos a hacer la comparación. Tendríamos las mismas palabras en cada vector, pero el doble de veces cada una, con lo que al calcular el nuevo vector multiplicando el valor de las coordenadas y luego sumándolas, obtendremos una similitud mucho mayor, lo que carece de sentido. Lo vemos en la Fig3.
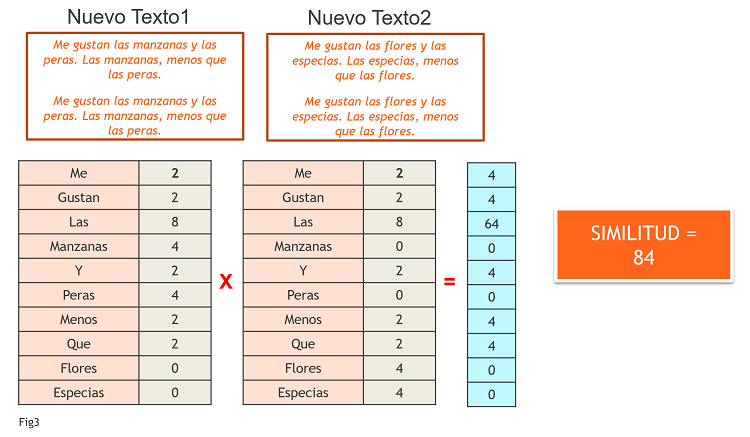
En matemáticas, siempre que el problema es la falta de comparabilidad por el tamaño la solución es fácil: relativizar el resultado a dicho tamaño. Hay diferentes formas de hacerlo. En este caso, donde lo que tenemos es un vector con varias coordenadas, una solución es dividir el valor de cada coordenada por la raíz cuadrada de la suma de las coordenadas al cuadrado (Fig4).
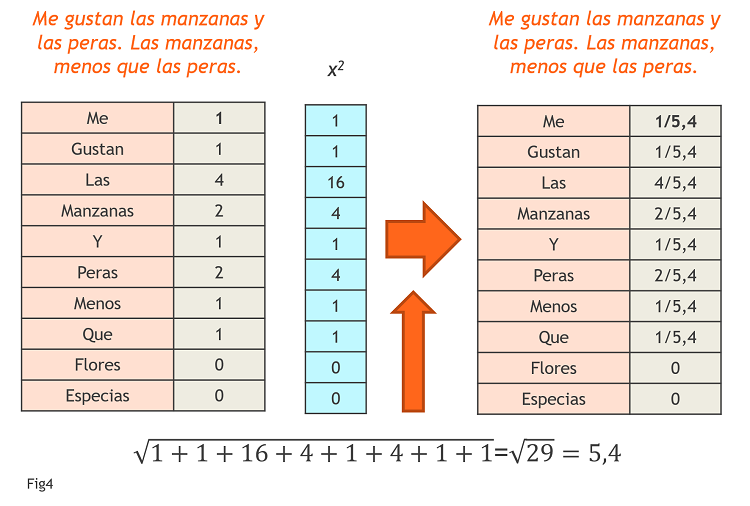
Si hacemos esto para los dos casos anteriores : 1) dos textos y 2) dos textos duplicados, el resultado de la similitud es el mismo en los dos casos (Similitud=0,72). Para diferenciarlo del anterior, lo llamaremos método de conteo relativizado.
Este método de conteo es sencillo de entender y fácil de aplicar. Sin embargo, a la hora de comparar textos que hablen de temas parecidos, sucederá que muchas de las palabras serán comunes a uno y otro texto, sumando esto al valor de la similitud y no siendo en realidad significativo. Por ejemplo, en los textos anteriores que hemos visto, la similitud venía dada sobre todo por palabras como “Me”, “Las”,»Y”, “Que”,… ¿Cómo conseguir no tener en cuenta esas palabras y sí las que son realmente importantes?
Hay un segundo método muy conocido (con un nombre un poco raro), el TF-IDF. TF son las siglas de Term Frequency, que es el vector de conteo que acabamos de ver. IDF son las siglas de Inverse Document Frequency, que va a ser un nuevo vector cuyas coordenadas van a tener que ver no solo con cada palabra sino también con la cantidad de documentos o textos que se analicen. Vamos a centrarnos en el cálculo del IDF. La fórmula que se aplica a cada coordenada es la siguiente:

Os explico el sentido de esta fórmula. El logaritmo es una función que tiene dos características interesantes:
- El logaritmo de números grandes es también un número grande
- El logaritmo de 1 es 0
¿Por qué es útil en nuestro caso? ¿Qué está haciendo esta función con cada una de las coordenadas del texto?
- Si la palabra es la típica que aparece en todos los textos, el numerador será un valor grande, pero también el denominador. Así que la división de uno entre el otro será algo parecido a 1. Al tomar el logaritmo de algo cercano a 1, el resultado será cercano a 0. POCO PESO A PALABRAS COMUNES.
- Si la palabra aparece en pocos textos, el numerador será un valor grande, y el denominador será pequeño. Por lo tanto, estaremos tomando el logaritmo de algo grande, que es también un valor grande. ALTO PESO A PALABRAS RARAS.
Siguiendo con nuestro ejemplo, supongamos que tuviéramos muchos casos similares, donde solo las palabras “manzanas” y “peras” apareciesen en 10 textos de un total de 1000 y el resto de palabras apareciesen en todos los textos. En la Fig6 vemos cómo sería el cálculo del TF-IDF.
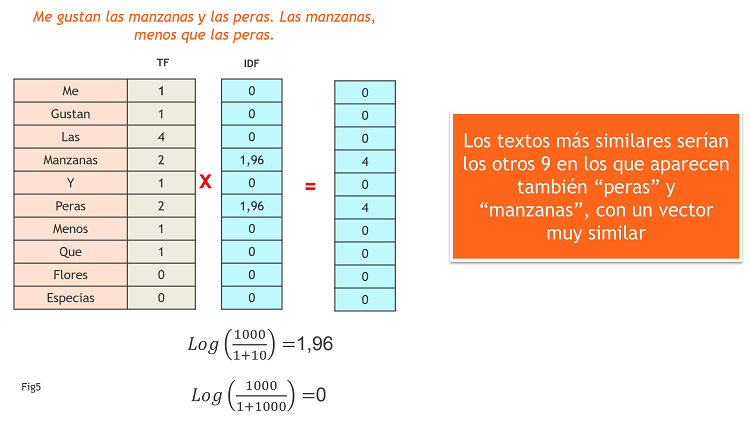
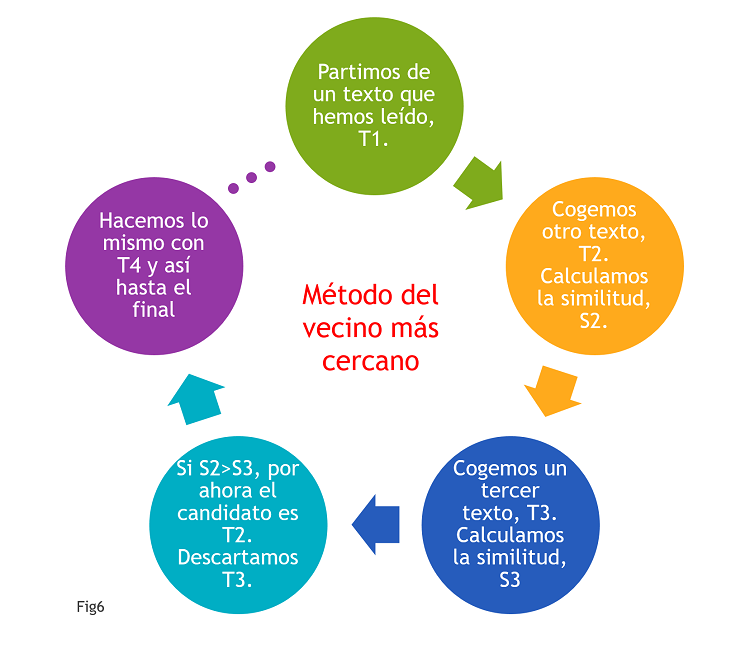
Este tipo de métodos que comparan textos se utilizan mucho para recomendar documentos o textos a personas que ya han leído otro texto. Una vez elegida la técnica, se utiliza lo que se conoce como «El método del vecino más cercano» para recomendar, de entre un montón de textos candidatos, aquel cuya similitud al texto inicial sea mayor. Vemos el funcionamiento de este método en la Fig6.




Comentarios